




Reed Solomon Galois Fields Theory

Home Reed Solomon Project Reed Solomon Galois Fields Theory Reed Solomon LABVIEW Implementation Reed Solomon Experiments
The Reed Solomon code is based on the theory of finite fields, named after the French mathematician as Galois fields (GF).
|
GALOIS FIELD PROPERTIES |
|
|
|
To describe GF Addition and Subtraction, a useful way to describe the GF elements is in polynomial form. In addition to representing GF elements in index form as above, each of the GF elements may be written as a polynomial of form: am-1xm-1 + ... +a2x2+ a1x1 + a0 where am-1...a0 take values 0 or 1. Thus, a GF element may also be described as a binary number am-1am-2...a1a0. By representing GF elements in binary form, GF addition or subtraction is implemented as the bit-by-bit exclusive-OR function of two binary numbers. Since addition and subtraction are synonymous in the exclusive-OR function of two binary numbers, minus signs in GF arithmetic may always be replaced by plus signs. |
Field generator polynomial p(x): Also known as the primitive polynomial, this is an irreducible polynomial (with no factors) of degree m. In this project, the predetermined value for m is 8. The following polynomial is used as the field generator polynomial: x8 + x4 + x3 + x2 + 1. As its name suggests, p(x) is used to construct all the field elements. It does so by using the fact that α is a root of p(x), i.e. p(α) = 0. Thus, α8 + α 4 + α 3 + α 2 + 1 = 0 or α8= α 4 + α 3 + α 2 + 1* *Minus signs are interchangeable with plus signs in GF arithmetic. |
Table 1 Galois field of 256 elements The last GF element is α254 since the maximum element in Galois Fields in αN-1where N = 2m - 1. In our case, m = 8 |
GF Multiplication: Multiplication in Galois field is the product modulo of p(x).
GF Division: GF Division is simply long division of GF elements in polynomial form. However subtraction at each stage to find the remainder is GF subtraction (which is the same as GF addition).
o Log of GF element is defined as follows: If αx= y then log(y)=x o Log-inverse of a GF element can be defines as follows: If αx= y then log-1(x)=y o Then GF multiplication is a●b = log -1( (log (a) + log(b) ) modulo p(x)) o And GF division is a/b = log -1 ( (log (a) - log(b) ) modulo p(x)) o a●0 = 0 and a/0 is undefined. |

Connecting Galois Fields Arithmetic to Reed Solomon Code
A Reed Solomon code may be described as RS(n,k) where
.png)
.jpg)
This project uses m = 8 bits/symbol and t = 8 symbols as these are the specified DVB-T (Digital Video Broadcasting-Terrestrial) standards. As Galois Field is the basis for Reed Solomon codes, GF(28) is the basis for our Reed Solomon code. A "shortened" RS code is implemented here where n <2m - 1. With n = 32 and t = 8, k = n - 2t or k = 16; so the RS code may be described as RS (32,16). RS codes are fundamentally block codes as opposed to convolutional codes. Block code is when data being transferred is divided into separate blocks. The RS Encoder adds parity symbols to each individual block which results in an output of the form
|
data |
parity |
data |
parity |
data |
parity |
... |
Reed Solomon codes are especially helpful for burst errors as all errors in a given symbol are counted only once, i.e. regardless of the number of bits in error in a symbol, RS code treats them as a single error, allowing yet seven more errors to be corrected if t = 8.

REED SOLOMON ENCODING
Our project with m = 8 contains 8-bit symbols and the GF has 28 or a maximum of 256 elements. When the RS Encoder adds 2t parity symbols to the original data of k symbols, 2t + k = n symbols are transmitted. RS Decoder at the receiver is then able to detect up to 2t symbols in error and correct up to t symbols in error. When the locations of symbols in error are not known, RS codes are able to correct up to half the number of parity symbols added. However, when the error locations are previously known (such errors are called erasures), RS codes can correct up to 2t erasures. A combination of errors and erasures may be corrected as long as the sum of these corrections is lesser than the number of parity symbols added.
RS(n,k) can be constructed when both the Encoder and the Decoder agree on a code generator polynomial g(x) which contains 2t factors and is defined as
g(x) = .png)
On the other hand, The Encoder considers the k symbol block as a polynomial M(x) of degree k-1. The Reed Solomon Encoder follows the below steps to construct a T(x) that contains n symbols (k + 2t symbols) for output by the Transmitter.
.jpg)

REED SOLOMON DECODING
Reed-Solomon Decoder considers the incoming message as a polynomial R(x), transmitted message as T(x), and the error introduced as a polynomial E(x). i.e.
.png)
Now the Decoder's job is to identify the E(x) so that T(x) can be calculated as follows:
.png)
Note that the minus sign is omitted because addition and subtraction are equivalent in GF arithmetic.
Syndromes
From our previous discussion in RS Encoding of how T(x) is formed, we know that T(x) is perfectly divisible by g(x). Thus, in the case that there are no errors for some i in [0, 2t-1], dividing by g(x) must evaluate to zero. However, when there are errors, some or all terms in g(x) will result in a non-zero value. This value is defined as a Syndrome or Si

.png)
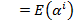 T(
T(.png) ) = 0 as x+
) = 0 as x+.png) is a factor of g(x) which is a factor of T(x)
is a factor of g(x) which is a factor of T(x)
.png) can be written in the form below where
can be written in the form below where .png) refer to the locations of the errors and the coefficients
refer to the locations of the errors and the coefficients 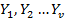 are the error magnitudes at these locations.
are the error magnitudes at these locations.
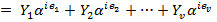
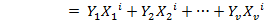
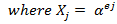
Error locator polynomial
Assuming 'v' is the degree of the error polynomial, the Error Locator Polynomial can be written as: 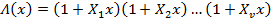
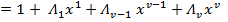
Roots of the above equation Λ(x) are .png)
Therefore we can write: 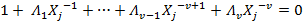
Multiplying both sides by 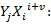
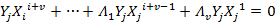
We can create similar error equation for different values of Xj. Terms collected together gives:...
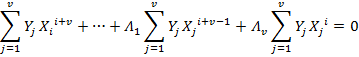
2t-v simultaneous equation can be derived by substituting 'I' with different values in [0, 2t-v-1]. Easiest way to solve the above equation is using Berlekamp's algorithm. Berlekamp's algorithm computes the coefficients of Λ(x) equation using following variables:

Berlekamp's Algorithm
Once the coefficients of Λ(x) are evaluated, finding 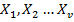 is easy because
is easy because 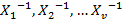 are roots of the equation Λ(x) and we also know that
are roots of the equation Λ(x) and we also know that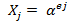
and j is in [0,n-1], where n is length of code. The Chien search method is applied on Λ(x) to identify Xj eventually for all ej. Chien search method evaluates a given polynomial for all possible roots; in our case the total is n. If equation evaluates to zero, then that value assigned to 'x' is considered as a root.
Prepared by Amulya Kattimani, a Rutgers ECE undergraduate student